広島大学生体システム論研究室では,長年にわたって生体信号のモデル化と識別に関する研究に取り組んできました.最近では,古居 彬先生(広島大学大学院先進理工系科学研究科情報科学プログラム 准教授)を中心に,筋電位や脳波,心電図などの統一的なモデル化を目指してスケールミクスチャモデル(尺度混合モデル)を開発し,医工学分野やヒューマンインタフェースへの応用を視野に入れて研究を行っています.
https://fka-bsys.hiroshima-u.ac.jp/news/18211
今回新たに,歪度を考慮したスケールミクスチャモデルを睡眠脳波の解析に適用した論文が掲載されました.この論文は,共同研究者の小川 景子先生(広島大学大学院人間社会科学研究科准教授)との共同研究の成果で,D3の畑元 雅璃君(筋電グループ,株式会社NTTドコモ)の博士学位論文の一部になる予定です.この論文誌 “Biomedical Signal Processing and Control”はELSEVIERから発行されているジャーナルで,Web of Scienceの”ENGINEERING, BIOMEDICAL”カテゴリーのQ1ジャーナル(Journal Impact Factor,Journal Citation Indicatorによるランキング)です.おめでとうございます!
今後も本研究チームとともに研究を継続し,さらなる研究成果につなげていければと思っています.
————————————————————————-
Non-Gaussian modeling of sleep EEG based on a skewed scale mixture structure and its application to sleep stage analysis
Miyari Hatamoto, Akira Furui, Keiko Ogawa, and Toshio Tsuji
(Miyari Hatamoto and Akira Furui contributed equally to this work.)
Biomedical Signal Processing and Control, Volume 109, 107947, https://doi.org/10.1016/j.bspc.2025.107947, Available online 5 May 2025 (SCIE, IF=4.9)
URL: https://www.sciencedirect.com/science/article/pii/S1746809425004586?via%3Dihub
<論文内容>
ハイライト:
(1) 睡眠脳波の非ガウス性を統一的に表現する確率モデル
(2) 最尤推定によりモデルパラメータを高精度に推定
(3) 複数の睡眠段階における多チャンネル脳波に対する高い妥当性
(4) 睡眠段階の変化に伴う非ガウス特性の有意な変化
目的:
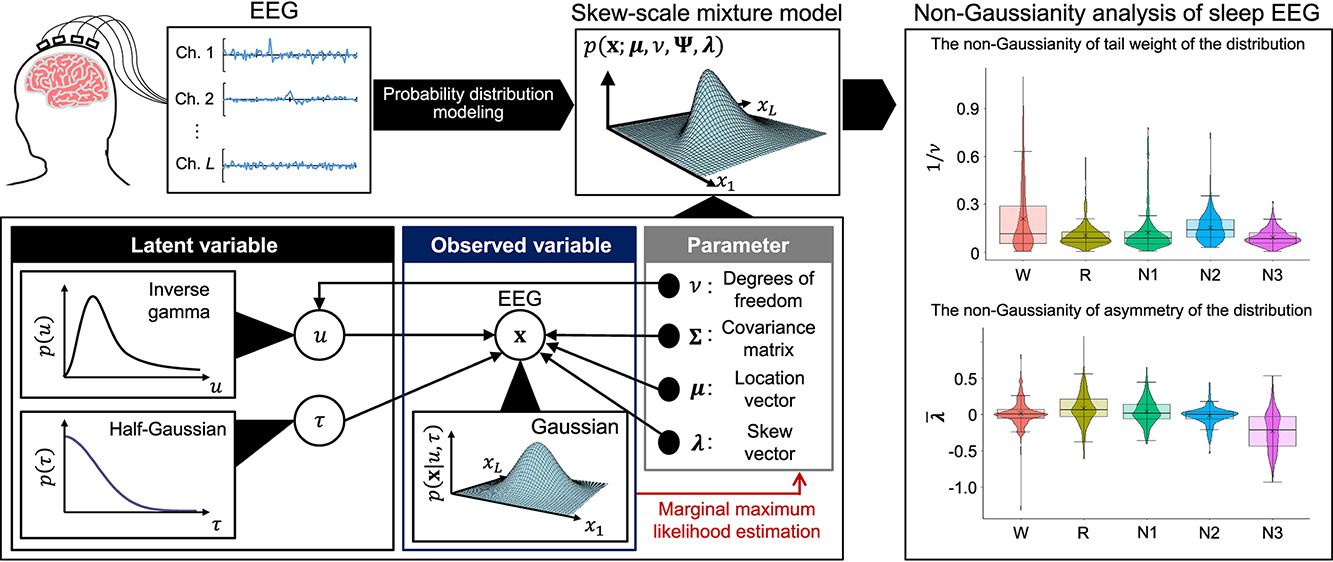
脳波は睡眠の評価に広く用いられている。脳波振幅分布の形状の変化は、睡眠段階を特徴付ける有用な指標となる。しかし、既存のモデルでは脳波の非ガウス特性を包括的に捉える表現力が不足している。
方法:
この問題に対処するため、我々は歪尺度混合構造に基づく新しいモデルを提案する。このモデルは脳波振幅を多変量ガウス分布に従う確率変数として扱い、その平均ベクトルと共分散行列はスケールと歪度パラメータによって重み付けされる。これらのパラメータは周辺尤度最大化を用いて推定され、テールウェイトや側方非対称性などの非ガウス特性を定量化する特徴量として用いられる。
結果:
提案モデルをシミュレーションにより検証し、覚醒、REM、N1、N2、N3の5つの睡眠段階を含むMontreal Archive of Sleep Studies(MASS)データセットの脳波データに適用した。従来の確率モデル(ガウスモデルやスケール混合モデルなど)と比較して、提案モデルはベイズ情報量基準(BIC)スコアによって評価されるように、非ガウス特性を表現する優れた能力を示した。さらに、抽出された特徴量は睡眠段階間で有意なばらつきを示し、徐波や紡錘といった睡眠段階特有の脳波特性を反映していた。
結論:
提案したスキュースケール混合モデルは、側方非対称性を含む睡眠脳波の非ガウス特性を包括的に表現する統一的な枠組みを提供する。
意義:
このモデルは、分類精度の向上や特徴的な波形の検出の強化といった応用の可能性を提供し、自動睡眠段階分類の将来的な発展の基礎を築くものである。
Highlights:
(1) The stochastic model that unifies the representation of non-Gaussianity in sleep EEG
(2) Model parameters are estimated with high accuracy by maximum likelihood estimation
(3) High validity for multi-channel EEG in multiple sleep stages
(4) Significant change in non-Gaussian characteristics with change in sleep stage
Objective:
Electroencephalograms (EEGs) are widely used to evaluate sleep. Changes in the shape of EEG amplitude distributions serve as useful indicators to characterize sleep stages. However, existing models lack the representational power to comprehensively capture the non-Gaussian characteristics of EEGs.
Methods:
To address this limitation, we propose a novel skew-scale mixture model based on a skewed scale mixture structure. This model treats EEG amplitudes as random variables following a multivariate Gaussian distribution, whose mean vector and covariance matrix are weighted by scale and skewness parameters. These parameters are estimated using marginal likelihood maximization and used as features to quantify non-Gaussian characteristics such as tail weight and lateral asymmetry.
Results:
The proposed model was validated through simulations and applied to EEG data from the Montreal Archive of Sleep Studies (MASS) dataset, which includes five sleep stages: wakefulness, REM, N1, N2, and N3. Compared to conventional probabilistic models (e.g., Gaussian and scale mixture models), the proposed model demonstrated superior ability to represent non-Gaussian characteristics, as evaluated by Bayesian Information Criterion (BIC) scores. Moreover, extracted features showed significant variation across sleep stages, reflecting stage-specific EEG characteristics such as slow waves and spindles.
Conclusion:
The proposed skew-scale mixture model provides a unified framework for comprehensively representing the non-Gaussian characteristics of sleep EEGs, including lateral asymmetry.
Significance:
This model offers the potential for applications such as improved classification accuracy and enhanced detection of characteristic waveforms, laying a foundation for future developments in automated sleep stage classification.
————————————————————————-